The content is published under a Creative Commons Attribution Non-Commercial 4.0 License.
Reviewed Article:
The Mechanics of Splitting Wood and the Design of Neolithic Woodworking Tools
Because of the anisotropy of wood, trunks and branches can be vulnerable to splitting along the grain, especially radially. This fact was widely exploited in pre-industrial times, when wood was mostly cut and shaped by splitting it along the grain while still green, rather than by sawing. However, splitting also remains a cause of potential weakness for wooden implements. To better understand the process of splitting wood, and the design of Neolithic tools, we model the force and energy required to split coppice branches both by hand, and by inserting wedges.
Introduction
In the Neolithic period, and indeed right up to the end of the pre-industrial age, the main way humans shaped wood was by splitting it. Narrow coppice poles and withies were split in half down their centre from Mesolithic times onwards by making a slit at the distal end with a blade or knife and then extending it by pulling the two sides apart with the hands (Bealer, 1996). Thicker rods could be split by pushing a blade such as a froe down the pole, levering the two sides of the rod apart (Bealer, 1996). Even logs as thick as tree trunks can be split, by hammering in wooden or antler wedges at the ends and along the sides of the log, and this has been performed from as far back as the Mesolithic period (Taylor, 2011). Half logs could be subsequently split into quarters using the same method and further splitting in the radial direction could make thinner and thinner planks and roof shingles (Bealer, 1996). The rods, withies and planks formed by this process are stronger and more waterproof than modern sawn planks since splitting between the longitudinal fibres and tracheids leaves no end-grain at its edges where cracks could start or where water could seep in. No doubt this has been one reason for the survival of a number of axe and adze handles (Evans, 1897; Sheridan, 1992; Taylor 1998; Harding 2014; Elburg, et al., 2015), Neolithic trackways (Coles, et al., 1973) and wells (Tegel, et al., 2012). However, this method cannot be used for all trees; it requires trees that have straight, knot-free trunks and branches of the sort that are found in trees growing in primary forest or in fast-growing coppice stands.
Pieces of wood were also shaped from Neolithic times onwards by asymmetric splitting, in which thin shards of wood were split off larger pieces. Logs had four sides removed (hewn) using adzes to square them up and c,arve their overall shape (Elburg, et al., 2015), while at increasingly small scales shavings were removed by drawknives, spokeshaves and planes (Bealer, 1996; Elburg, et al., 2015).
Many authors have investigated how Neolithic axes and adzes would have been used to cut down trees (Jørgensen, 1985; Mathieu and Meyer, 1997; Elburg, et al., 2015). It is clear from the results of such experiments, that trees are best felled with such implements by hitting the trunk at an acute angle, so that much of the stroke actually involves cutting the wood along the grain.
However, despite the importance of splitting wood in prehistoric times, little effort has been made to work out why wood was shaped in this way, rather than by sawing it. Nor is it known how effective Neolithic axes and adzes would have been at splitting wood, or the factors that underlie their design. But to understand this we first of all need to know more about the material properties of wood and the process of splitting it. This paper starts out by reviewing the structure of tree trunks and branches, therefore explaining why wood is so easy to split, something that can be a problem for the trees for which it is of course the main structural material. The paper then develops a simplified analysis of the symmetrical splitting of a coppice rod, a branch or a long log. It investigates the mechanics of the process from first principles and estimates the forces and energy changes needed. It first looks at the simplest case of all - that of splitting a rod by pulling two sides apart. This is followed by the rather more complex case of splitting the rod by inserting a wedge. This analysis was necessary to make predictions about the process and to design experiments in which coppice poles were split using these two methods. These experiments test the predictions of the models and cast light on the best way to split wood and the optimal design of Neolithic woodworking tools. However, those of a non-mathematical disposition can safely ignore the maths and simply look at the predictions of the model, which are given in simple English. The paper ends with a discussion of the implications of the test results for Neolithic tool design.
Wood Structure and Mechanics
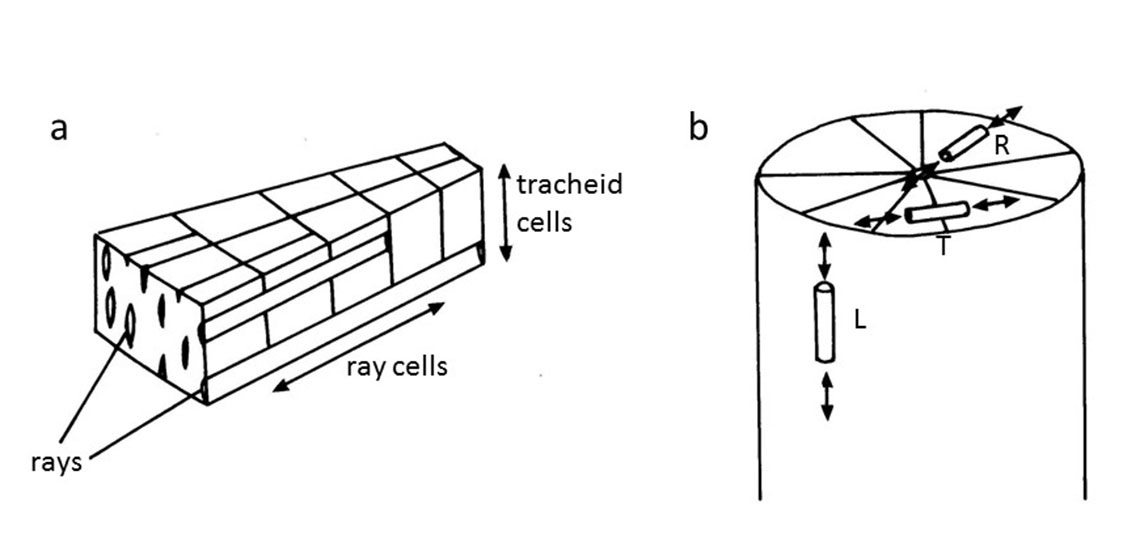
It is well known that the arrangement of cells in wood gives it highly anisotropic mechanical properties. The great majority of the tissue, (80-98%) is composed of long narrow tracheids or fibre cells that are orientated longitudinally up and down the trunk and branches (Hoadley, 2000; Ennos and van Casteren, 2010) (See Figure 1). Broadleaved trees also have some wider narrow-walled vessels which help transport water up the trunk more efficiently than narrow tracheids. The only other cells are the ray cells which form spindle-shaped rays that run radially, from the pith to the bark, and which reinforce the trunk in this direction (See Figure 1) effectively pinning the growth rings together.
A wooden branch is very hard to break across the grain because this involves fracturing the tracheids. In contrast, it is easily split along the grain, especially radially down the centre of the branch, as this just involves separating the tracheid cells. Fracturing the branch tangentially is slightly harder as this involves breaking through the ray cells. Wood is consequently 8-10 times stronger longitudinally than transversely, and most types of wood are also 20-50% stronger in the radial direction than in the tangential direction because of the reinforcement by the rays (Reiterer, et al., 2002; van Casteren, et al., 2012).
The toughness of wood - its ability to absorb energy when broken - shows even greater anisotropy; the work of fracture across the grain (breaking through the tracheids) is in the order of 50-100,000 Jm-2, around 50-100 times greater than the work of fracture along the grain which is in the order of 200-2,000 Jm-2. The work of fracture in the radial direction is also typically 20-50% higher than in the tangential direction because of the energy required to break through the rays (Reiterer, et al., 2002; Özden and Ennos, 2014; Özden, Ennos and Cattaneo, 2017).
Splitting in Trees
Splitting can therefore be a problem for the branches of trees, even though the bending forces set up by gravity and the wind largely set up forces parallel to their long axes. Upwardly bent branches constitute what Mattheck called “hazard beams” which can split down the centre under their own weight due to the vertical tensile forces set up in the branch (Mattheck and Kubler, 1995; Ennos and van Casteren, 2010). Branches which are being broken across also tend to split down their centre, undergoing what is known as a ‘greenstick fracture’ (Ennos and van Casteren, 2010, van Casteren, et al., 2012). This process prevents the branch from being detached. Splitting can also be a problem for tree forks, which break apart when the two arms are pulled apart along the centre of the fork at significantly lower forces. Recent research has shown that the join between the two arms of the fork are strengthened by the interlocking grain (Slater, et al., 2014; Slater and Ennos, 2015).
Mechanical Theory
Despite the importance of splitting wood by early humans, there is little information about the forces and energy required or even a real understanding of the splitting process itself. The process by which some anisotropic materials are cut has been investigated theoretically and experimentally by materials scientists (Obreimoff, 1930; Gurney and Hunt, 1967; Atkins, 2009; Williams and Patel, 2016). However, they have mainly been interested in the highly asymmetric processes of planing or cutting veneers. These authors have concentrated on the steady state case long after the initiation of splits and they use a complex notation that is not readily accessible to biologists. The following presents a new simplified theory of splitting in wood.
Simple Splitting
Consider the situation shown in Figure 2a, in which a crack has been started down the centreline at the distal end of a coppice pole, and the two ends are being pulled apart. A force, F, is needed to bend the two ends and to drive the crack forward through the pole. The distance down the pole, x, and the crack is driven for a given displacement, y, of each half is best determined by considering the energy expended. The further the crack extends (and hence the higher value of x), the greater the energy required to split the wood and create two new fracture surfaces. However, the further the crack extends, the smaller would be the force needed to bend the two halves and the less elastic energy would be stored within them. Typically, material deforms in the way in which energy expenditure is minimised, therefore the crack will extend until the sum of these two forms of energy is minimised. The stored elastic energy in the bent halves is progressively used to open the crack as the two halves are pulled apart.
Formally, the energy used to pull the two halves a distance 2y apart is given by the following mathematical expression, where the first part is the energy required to split the wood while the second part is the energy to bend the two halves (1):

Where r is the radius of the pole, Gf is the work of radial fracture of the wood along the pole, x is the length of the crack, F is the force required and y is the displacement of each half. The force ( F ) required to deflect a cantilever by a distance y is given by the formula (2):

E is the Young’s modulus of the wood in the longitudinal direction and I is the second moment of area of each hemicylinder. Combining equations 1 and 2 we get (3):
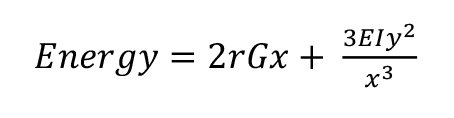
The energy is minimised when the differential of energy with respect to x is zero, thus (4a)
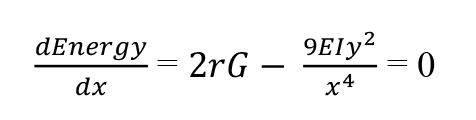
and (4b)
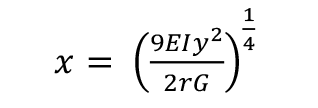
And since the second moment of area I of a half cylinder is given by the equation (5)
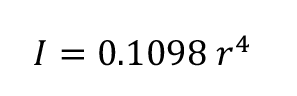
Then (6)

The length of the crack, x , should therefore rise in proportion to the square root of the displacement, y , with the Young’s modulus, E, to the power of one quarter , with the radius of the pole to the power ¾, and fall with the fourth root of the work of fracture, Gf, (See Figure 2b).
The force required, F, can be found by inserting the expression for x into equation 2, so that (7)
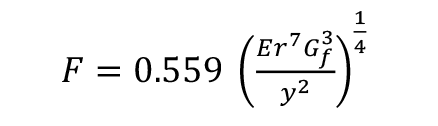
The force required will rise with stiffness to the power of a quarter, to radius tothe power of 7/4, to work of fracture to the power of ¾ and fall with the square root of the displacement (See Figure 2c).
Predictions of the Hand Splitting Model
The analysis has a number of somewhat surprising predictions (See Figure 2). First, because the crack length increases with the square root of displacement, the crack should lengthen rapidly at first as the two ends are pulled apart, but less quickly later on; as a consequence the force needed to open the crack will actually be greatest at the start and fall away with the square root of the displacement. The force required will also increase slowly with the stiffness of the wood, but it will be far more affected by its work of fracture and radius; thick rods with high work of fracture will be far harder to split. It should also be noted that three quarters of the energy used at any time is to extend the crack with only a quarter used to bend the arms of the end cantilevers.
Moments on and Stresses within the Arms
The moment, M, required to split the pole is given by the expression (8):
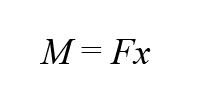
So combining equations 6 and 7 (=9):
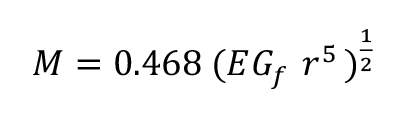
The moment is independent of the length of the crack or displacement of the two ends, but will increase with the square root of both the Young’s modulus and the work of fracture and also to the radius to the power of 5/2. Therefore, thicker rods will be much more resistant to splitting and the resistance will be greater in stiffer, tougher wood.
The moment will set up longitudinal stresses along each side of the rod: tensile stresses on the internal surface and compressive ones on the external surface. Since the centroid of a semicircle is closest to the internal surface the maximum stress σmax will be a compressive one and will be given by the expression (10):
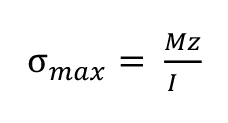
Where z is the distance of the centroid of area of each semicircle to the outer surface, which is 0.576 r, so combining equations 5, 9 and 10 (=11):
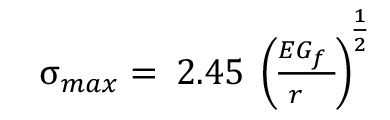
The stresses will fall with the square root of the radius. Consequently, thicker rods will be less stressed longitudinally when split than narrow ones.
Splitting Wood Using Wedges
When the two arms of the coppice pole are opened, not by pulling them apart, but by inserting a wedge that prises them apart, the mechanics becomes somewhat more complex and the energy required increases.
As a wedge with an internal angle of 2θ is inserted a distance z into the end of the pole (See Figure 3) the upper end will be moved up a distance, y, where (12)
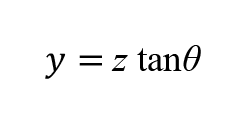
So, the length of crack is (13):
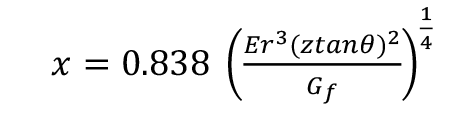
The length of the crack, x , should therefore rise in proportion to the square root of the insertion distance of the wedge but also with the square root of the tangent of the angle θ .
The force, P, required to push in the wedge in the absence of friction can be determined readily by trigonometry, considering that (14)
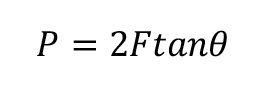
So that (15)

And rearranging (16)

The force required will rise with the square root of the angle θ and fall with the square root of the insertion distance, z .
However, the insertion of the wedge will also be resisted by the friction, G, between the blade and the rod, which by trigonometry is equal to (17)
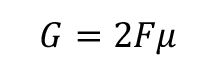
where μ is the coefficient of friction between the wedge and the wood so that (18)

Thus, the total force resisting the wedge is given by the expression (19):
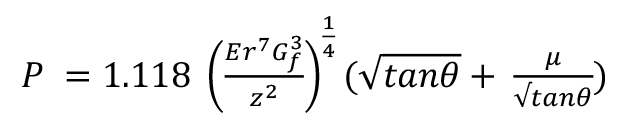
Just as for splitting a coppice pole by pulling it apart, the force required to split it by inserting a wedge will rise with stiffness to the power of a quarter, to the radius to the power of 7/4, to work of fracture to the power of ¾ and fall with the square root of the insertion distance. However, it will also vary with the angle of the wedge (See Figure 3b). The force to create new fracture surfaces and bend the arms will rise with the wedge angle, because blades inclined at higher angles will push the crack further forward for a given insertion distance. In contrast, the friction force will fall with the angle. This is because the normal force needed to push the arms apart will fall more quickly with the insertion distance because the ends of the arms will be further behind the tip of the crack and the normal force required will be less.
Of course, this analysis assumes that the ends of the arms subtend a low angle, and touch the blade at their ends (See Figure 3). If real wedges are inserted, one of two things will eventually happen. In long wedges, the arms will eventually lie flat against the wedge (See Figure 4). In contrast, in wedges with a limited width, the arms will eventually touch the wedge at the back of the widening section (See Figure 5). In both cases, further forward movement of the wedge will result in the crack moving forward at the same speed as the wedge and at a constant force.
The angle that the rear end of the arms of a cantilever subtends is three times the average angle of the cantilever (Gordon, 1978). Therefore, for a long wedge of angle θ, the arms will lie flat against the wedge when z = x/3
So when (20)
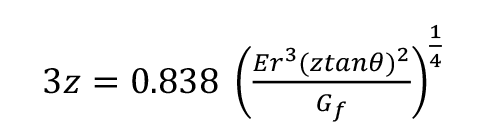
And rearranging (21)
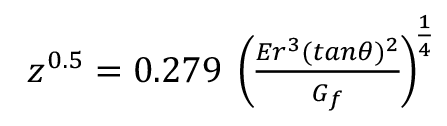
So that the greater the angle, θ , of the wedge, the further it can be inserted before the arms lie flat and the force stops falling (See Figure 4a-c). Note that the greater the angle of the wedge, θ , the lower the force P to continue opening the crack, because the point at which the arm touches the wedge will be further from the crack tip; the restoring force F will therefore be lower and consequently so will the friction G resisting the movement of the wedge. Therefore, wider wedges will initially be harder to insert but after a time become easier (See Figure 4c).
For a short wedge of half-thickness,t, the change will occur at an insertion distance, z, of (22)
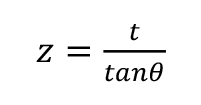
so that as t becomes larger, the greater is the insertion distance at which the force stops falling (See Figure 5c). Thereafter, the restoring force, F , will be lower and the force P required to continue opening the crack will fall to a lower constant value because of reduced the friction.
Predictions of the Wedge Splitting Model
The mathematics therefore makes certain predictions about the force and energy needed to wedge open coppice poles. Firstly, for all wedge designs, the maximum force needed will initially rise rapidly to a maximum, before falling off. Secondly, the maximum force required will be greater in wider angle wedges. However, the force will fall further in wider angle wedges, to a lower constant value because of reduced friction between the wedge and the wood, so that the energy required to produce a given length of cut will be lower (See Figure 4c). The force will also fall further in broader wedges to a lower constant value because of reduced friction between the wedge and the wood (See Figure 5c), so that the energy required to produce a given length of cut will be lower. Finally, the higher the coefficient of friction between the wedge and the wood the greater will be the force and energy required to split the wood.
The theory therefore makes several predictions that can be tested by carrying out a series of tests in which poles are split either by pulling the two halves apart directly or by wedging them apart with wedges of contrasting design. It was decided in this first study to perform the tests on relatively narrow coppice poles of hazel, ranging from 10-15 mm in diameter. Such poles were chosen for several reasons: (i) coppice poles are regular in form and have straight grain, and so split relatively easily; (ii) the forces involved are sufficiently small to allow the tests to be performed in a small universal testing machine involving forces of no more than 500 N; (iii) these green poles are typical of those split by humans before the industrial age and were used to make wickerwork structures such as hurdles, wattle wall panels and tracks; (iv) hazel was also the wood used by Slater (Slater et al, 2014; Slater and Ennos, 2015) to investigate the splitting of tree forks, so the results from this study should also help illuminate how those trees reinforce their fork junctions against splitting.
Materials and Methods
Coppice Poles
Coppice poles of hazel (Corylus avellana) were cut from Beverley Community Wood, Beverley, United Kingdom, from trees that had last been coppiced five years before and kept moist until used. Poles were approximately cylindrical, 13.24 ± 0.69 mm in diameter and were 3-4 years old.
Pulling Tests
Ten coppice rods, 20 cm long, were cut from the poles with the distal 10 cm free of leaf scars or knots to obtain a length of wood with parallel grain. A hole of diameter 2 mm was cut 5 mm from the distal end of each rod and a central notch cut down 5 mm from the tip at right angles to the hole to give a starting crack for the splitting of the wood. 1 cm long wood screws were then screwed into either end of the hole, with their tips almost touching at the centre of the rod. This gave a firm attachment which could be gripped to pull the two ends apart.
The two screws were then inserted between the upper and lower corrugated jaws of an Instron 3401 universal testing machine. The upper jaw was then moved upwards at a speed of 50 mms-1, to split the rod down its length, while the force required was measured using a 1 kN load cell. The force and displacement were simultaneously recorded on an interfacing computer. The test was ended when the upper jaw had moved upwards a distance of 20 mm, and the energy required to split the wood was calculated by measuring the area under the force-displacement curve. The distance that the pole had split was measured using a ruler, allowing the energy per unit area of split to be calculated.
Wedge Tests
Wedge Design
Nine wedges of contrasting design were constructed from mild steel in the Department of Chemistry’s workshops. All the wedges were 40 mm long and 20 mm wide, but had a range of cross sections and surface textures to give variability in three different attributes.
1. Variation in Angle
Seven wedges were made with a triangular cross section but with different blade angles. Blades were cut at included angles of 7°, 10°, 15°, 20°, 25°, 30°, and 40°, giving basal widths of 4.9 mm, 7.0 mm, 10.5 mm, 14.1 mm, 17.7 mm, 21.4 mm and 29.1 mm.
2. Variation in Width
Another three wedges were made which included angles of 20°, but with the bevel extending only 10 mm, 20 mm and 30 mm from the tip, giving basal widths of 3.5 mm, 7.1 mm, and 10.6 mm.
3. Variation in Surface Roughness
Finally, the faces of the 15° blade were milled to give rough surfaces with ridges in the order of 0.5 mm deep.
Wedging Tests
For each set of wedge tests, twenty coppice rods 20 cm long were cut from the poles, with the distal 10 cm free of leaf scars or knots to obtain a length of wood with parallel grain. A central notch cut down 3 mm from the tip to give a starting crack for the splitting of the wood. The rod was then mounted vertically, being held firm within the lower jaws of the Instron. A wedge was then mounted using blu-tack onto a compression plate mounted on the upper arm of the Instron, and lowered so that the blade was inserted into the starting crack of the rod and just touching it. The upper arm was then moved downwards at a speed of 50 mms-1, causing the blade to split the rod down its length, while the force required was measured using a 1 kN load cell. The force and displacement were simultaneously recorded on an interfacing computer. The test was ended when the blade had moved downwards a distance of 30 mm, and the energy required to split the wood was calculated by measuring the area under the force-displacement curve. The distance the rod had split was measured using a ruler, allowing the energy per unit area of split to be calculated.
Results
Pulling Tests
In the pulling tests, the force required to split the wood rose rapidly initially to a peak, the mean peak force being 106.6 ± 12.2 N, at a displacement of 0.78 ± 0.15 mm, before falling off rapidly thereafter (See Figure 6). The split also travelled rapidly along the wood at first, as predicted, before slowing down progressively until, at the final jaw displacement of 20 mm, the split had travelled a mean of 91.7 ± 21.4 mm down the rod and the force had fallen to 15-20 N (See Figure 2). The mean energy required was 0.570 ± 0.40 J, giving a mean work per unit area of split of 501.7 ± 122.8 Jm-2.
The shapes of the force-displacement curves were analysed to determine whether the force fell as predicted with square root of the jaw displacement. A linear regression was carried out for all 10 rods of the log10(force) vs log10(displacement) for all displacements from 2 mm (well after the peak force had been reached) up to 20 mm. The mean slope of the 10 curves was -0.527 ± 0.125. A one-sample t-test showed that the mean slope was not significantly different from the slope predicted by the splitting theory of -0.5 (t(9) = 0.618, p = 0.513).
Wedge Tests
In all the wedge tests, the force required to split the wood rose rapidly initially but fell off quickly thereafter, like the pulling tests. The split also travelled rapidly along the wood at first, as predicted by the splitting theory, before slowing down progressively leading to a final length of cut of between 35 and 140 mm. Longer splits on average were seen when the rods were cut with wider angle and broader wedges. However, there were notable differences in the shape of the force deflection curve, the maximum force required, and the energy needed, depending on the design of the different wedges.
The Effect of Angle
There were marked differences in the shapes of the force displacement curves for wedges of different angles. For low angles, the force rose relatively slowly at first, reaching a maximum at 2- 5 mm, and only fell slowly thereafter (See Figure 7). In contrast, for the high angles the force rose more rapidly to a higher peak at a displacement of only 1-2 mm, but fell much more rapidly after that. The two sets of curves therefore crossed over each other as predicted by theory (See Figure 7).
There were also differences in the maximum force required between wedges of different angle (See Figure 8a); blades with higher angles required in general a greater maximum force. A one- way ANOVA showed that these differences were highly significant (F6,63 = 5.60, p < 0.0005), Tukey tests showing that the maximum force for the 30° wedge was significantly higher than those at 7° (p = 0.001), 10° (p = 0.018), 15° (p < 0.005), and 20° (p = 0.045), while the maximum force for the 40° wedge was significantly higher than the 15° wedge (p = 0.044).
Wedges of different angles also drove the crack different distances along the rods (See Figure 8b), blades with higher angles driving the crack further down the rods. A one-way ANOVA showed that these differences were highly significant (F6,63 = 28.03, p < 0.0005).
The effect of angle on the energy required per unit area of split was even more pronounced (See Figure 8c), but in this case blades with lower angles required more energy. Once again a one-way ANOVA showed that these differences were highly significant (F6,63 = 38.46, p < 0.0005), Tukey tests showing that the energy per unit area for the 7° wedge was significantly higher than all the others (p < 0.0005 in all cases), while the energy per unit area for the 10° wedge was higher than those at 15°, 20°, 25°, 30°, and 40° (p < 0.0005 in all cases).
The Effect of Width
There were marked differences in the shapes of the curves for blades of different widths. At low displacements, the shape of the curves was similar but at higher displacements differences emerged. For the narrower blade, the force stopped falling sooner and remained higher until the end of the test relative to the broader blade.
There was no significant difference in the maximum force required between blades of different width (See Figure 9a) (F2,27 = 0.14, p = 0.872). There were however, significant differences in the distance the cracks were driven (See Figure 9b) (F2,27 = 3.62, p = 0.041); Tukey tests showed that the 10.6 mm wedge drove cracks significantly longer than the 3.5 mm wide wedge (p = 0.023). There were also significant differences in the energy required per unit area of split (See Figure 9c) (F2,27 = 6.91, p = 0.004); in particular the mean energy per unit area for the 3.5 mm wide wedge was 48% higher than the 10.6 mm wide wedge, a difference that a Tukey test showed was significant (p = 0.003).
The Effect of Surface Roughness
Roughness had no noticeable effect on the shapes of the force displacement curves or the distance the cracks were driven. However, an independent sample t test showed that it did have significant effects on both the maximum force and energy required per unit area to split coppice (See Figure 10). Rougher blades required a 50% higher maximum force (t(18) = 2.67, p = 0.016) and used 98% more energy per unit area (t(18) = 8.10, p < 0.0005).
Discussion
The results of the hand splitting tests agreed well with the predictions made by the mathematical model, both qualitatively and quantitatively. In both sets of tests, the crack ran rapidly down the pole initially just as predicted and the force quickly rose to a peak falling thereafter as the speed of crack propagation slowed. Regression analysis on the pulling tests showed that the force fell with the square-root of the displacement, as predicted by the mathematical model.
The mathematical model also allowed us to estimate the radial work of fracture of the coppice wood from the results of the pulling tests. The energy needed to split the rods in such tests was 501.7 ± 122.8 Jm-2, but according to the analysis only three quarters of this would have been used to extend the crack, giving a work of fracture, Gf , of 376.3 ± 92.1 Jm-2. This is well within the values for hardwoods (Reiterer, et al., 2002; Özden and Ennos, 2014; Özden, Slater and Ennos, 2017).
The results of the wedge splitting tests also agreed well with the predictions made by mathematical model about the effect of the form/shape of the wedge on the splitting process. Firstly, the forces were initially greatest for the high angle wedges because they pushed the arms of the pole apart more rapidly and initially drove the crack forward faster through the wood. However, the forces fell further in the wider angle and thicker wedges because the crack tip was driven further in front of the blade, resulting in a lower force to push apart the two arms and hence lower friction. This resulted in a highly counterintuitive result; wider and thicker wedges were more energetically efficient cutting tools; one would normally expect sharper, thinner cutting blades to be more efficient. The smoother wedge was also more efficient than the rough one, probably because of its lower friction, a finding that does agree with our intuition. These results also emphasise the overriding importance of friction in resisting wedge splitting. The energy per unit area needed to split wood with a wedge ranged between 1,400 and 4,200 Jm-2, several times that needed to split wood by simply pulling on the two arms; this difference must have been due to the friction. The effect of friction was also responsible for the intuitively surprisingly greater efficiency of the broader and wider-angle wedges, and the less surprising advantage shown by the smoother blade.
These results also have important implications about how early woodworking tools are designed to split wood; and how early wooden implements themselves were designed to avoid splitting.
Splitting and the Design of Woodworking Blades
Understanding the mechanics of splitting wood enables us to better understand the ways in which humans have shaped it. Firstly, the results of the analysis and of the tests shed light on the techniques used by woodsmen to hand-split narrow coppice poles like the ones we used. They insert a froe into the distal end of the coppice pole to start the crack and then use the blade to lever it open (Bealer, 1996). This enables them to overcome the high initial forces that resist splitting, after which they can hold the two ends and pull them apart to efficiently continue the process.
Secondly, the model can help us understand why people have used wedges from the Mesolithic onwards to split thick branches; the force needed to split branches should rise with radius to the power of 1.75, making hand splitting of thicker branches and trunks impossible, so wedges would be needed for branches more than a few millimetres thick. Unfortunately, using wedges is less energetically efficient than hand splitting because it is also resisted by friction between the wedge and the wood.
The results of the analysis and of the wedge tests we performed also shed much light on the mechanical design and use of both modern and ancient wood cutting implements. The most important finding was that friction dominates the process of splitting wood with wedges, and that this can be minimised by using smooth, wide angle blades. This explains why broad heavy splitting mauls, with an included angle of 30-35° are nowadays greatly preferred for splitting logs over narrow-bladed felling axes. The latter will not only be less efficient, but are notoriously prone to getting stuck into wood (Bealer, 1996; Mytting, 2015) because of the high normal and friction forces on their narrow blades.
The results also explain why traditional carpentry tools that are designed to split wood along the grain, such as planes, drawknives and spokeshaves, are used with the blades held at such large cutting angles (Bealer, 1996); the inclined blades keep the tip of the split well in front of the blade, reducing friction between the blade and the shavings. Of course, this process is different from splitting coppice, as it is asymmetrical; one arm, the shaving, is much thinner than the main piece of wood from which it is detached, but the mechanics must be very similar.
Most interestingly, however, these results illuminate the design of early stone axes and explain the dramatic changes that occurred between the Mesolithic and Neolithic periods in the design of the axe heads themselves (Evans, 1897; Yerkes, et al., 2003; Barkai and Yerkes, 2008). Mesolithic tranchet axe heads were typically made of thin shards of flint with a sharp cutting edge that was formed by a flaking process. In contrast the Neolithic axe head, which could be formed from flint or igneous rock, was much broader and heavier and had a wider-angle blade. The cutting edge was not very sharp, but the side of the blades were ground down by a laborious polishing process into a smooth finish. These differences would have suited the two types of axe to quite different mechanical functions. The Mesolithic axes would have been good at cutting soft tissue, but with their rough, narrow blades they would have readily got stuck in wood if used for splitting it. The Neolithic axe, on the other hand, with its broad smooth head, would seem to be ideally suited for efficiently splitting wood. It would have been much more useful for the new settled farming lifestyle of Neolithic people, who needed to clear woodland for their crops and to split and shape wooden beams and branches to build their new settlements and trackways. The lack of a sharp cutting edge would have been no problem since the tip of the blade would usually never touch the wood.
Of course, Neolithic people would also have had to use their axes to cut across the grain of wood to enable them to cut down trees. Experimental archaeological investigations suggest that the broad Neolithic axes were in fact most effective when they were used to cut obliquely up and down the trunk, so that they acted partly to cut across and partly to split the wood (Jørgensen, 1985; Mathieu and Meyer, 1997; Elburg, et al., 2015). For this reason, we plan future tests in which the effectiveness of blades of different design is investigated when they are used to make just such oblique cuts.
Finally, the model explains the greater difficulty in shaving off ever thinner flakes of wood, and the change in form of the shavings. As the model shows and as materials scientists studying veneers have shown (Atkins, 2009; Williams and Patel, 2016), longitudinal stresses set up by wedges increase as the thickness of the piece to be removed decreases. Eventually such longitudinal stresses will exceed the yield stress of the wood in compression, causing the shavings to curl. In even thinner cuts, the wood will break longitudinally, resulting in removal of a series of chips.
Splitting and the Design of Axe and Adze Handles
Unlike trees, which avoid having loose ends of grain where splits can develop, wooden tools such as axe and adze handles leave the end grain of wood exposed. They are therefore prone to failure by the process of splitting along the grain, so the analysis presented here can also shed light on how such structures should be designed to be more robust.
Firstly, one of the main problems of axe handles which are cut with tenons to hold the blade is that they are prone to splitting along their length (See Figure 11a-c). One main finding of our previous research on the tangential properties of wood is that it has a higher work of fracture against tangential splitting than radial splitting (Özden and Ennos 2014; Özden, Ennos and Cattaneo, 2017). In modern axes the handles are carved so that the growth rings are parallel to the blade of the axe (Bealer, 1996). Consequently, when the distal end is notched and a wedge inserted to open it out and grip the blade, extension of the notch is resisted by the rays within the wood. In a similar way, Neolithic axes in which the handle is cut with a tenon to hold the blade would also be expected to be carved in the same way (See Figure 11b): with the tenons cut parallel to the growth rings.
The analysis can also explain some of the characteristic features of Neolithic axe handles. In many of these, the distal end of the handle is thickened (Harding, 2014), and incorporates flanges at the two ends of the tenon (See Figure 11b-c). These features should increase the splitting resistance at the ends of the tenon and so greatly strengthen the handle. The fact that this was such an important consideration can be seen in the Etton axe handle (Taylor, 1998) (See Figure 11a) in which one side of the handle had totally split off.
Second, we can start to understand why so many Neolithic adze handles and bronze-age axe handles were made from the forks of trees or the joints between side branches of trees and the trunk (See Figure 11e). This avoids the weakening caused by cutting a tenon in the handle and it exploits another aspect of the mechanical design of trees. Tree forks are specially designed to resist splitting; the grain is arranged to interlock or be whorled (Slater, et al., 2014; Slater and Ennos, 2015) an arrangement that greatly strengthens them, and increases the transverse work of fracture by a factor of around 4 (Özden, Slater and Ennos, 2017). Neolithic ards made similar use of such joints in trees to make strong structures with a complex, bent shape.
Conclusion
In conclusion, our splitting model has made predictions, some of them quite counterintuitive, that have been validated, both qualitatively and quantitatively by our series of splitting tests on hazel coppice. The model sheds new light on the cutting blades of early human woodworking tools such as axes and adzes and their wooden handles. However, the results so far have barely scratched the surface of this topic. More quantitative research needs to be performed on the effect of shape, size, hydration, as well as wood anatomy and density on the splitting failure of wooden structures by natural occurrences and those shaped by humans.
Acknowledgements
We thank Nigel Parkin for making the steel wedges and East Riding of Yorkshire council for access to the hazel coppice.
Keywords
Country
- United Kingdom
Summary
Because of the anisotropy of wood, trunks and branches can be vulnerable to splitting along the grain, especially radially. This fact was widely exploited in pre-industrial times, when wood was mostly cut and shaped by splitting it along the grain while still green, rather than by sawing. However, splitting also remains a cause of potential weakness for wooden implements. To better understand the process of splitting wood, and the design of Neolithic tools, we model the force and energy required to split coppice branches both by hand, and by inserting wedges. The models predict that a high initial force is required to split the branches along their length but that the speed of crack propagation and the force required both fall as the process proceeds. The models also predict that splitting using wedges will take more energy because of the friction between the wedge and the wood. A greater initial force is needed for wider angle blades because they drive the crack forwards faster, but the force will fall further because the contact point with the wood moves further back from the crack tip. Counterintuitively, therefore, broad, blunt blades should use less energy to split wood because of the lower friction they encounter and smoother blades should use be more efficient than rough ones. The model was tested by splitting coppice poles of hazel in a universal testing machine, both by pulling them directly apart and by inserting steel wedges of contrasting angle, thickness and roughness. The results agreed well with the predictions of the model and help explain several aspects of the design of traditional and Neolithic woodworking tools, and the wooden handle of the tools themselves. Firstly, the smooth wide angled blades of Neolithic axes and adzes would help them split wood more efficiently, like modern splitting mauls and woodworking planes. Secondly, the shape of the Neolithic axe handles would have been well suited to prevent them splitting, and having the growth rings parallel to the blade would have further improved their splitting resistance. Thirdly, the design of Neolithic adzes handles and ards, often made from the branch junctions and forks of trees, would have exploited the trees’ own design to resist splitting at the branching point; interlocking and whorled grain.
Bibliography
ATKINS, T., 2009. The Science and Engineering of Cutting: The Mechanics and Processes of Separating, Scratching and Puncturing Biomaterials, Metals and Non-Metals. Amsterdam:Elsevier.
BARKAI, R. and YERKES, R.W., 2008. Stone Axes as cultural markers: technological, functional and symbolic changes in bifacial tools during the transition from hunter-gatherers to sedentary agriculturalists in the Southern Levant. Prehistoric Technology , 40, pp. 159-167.
BEALER, A.W., 1996. Old Ways of Working Wood: Techniques & Tools of a Time-Honored Craft. Edison, N.J.: Castle Books.
COLES, J.M., HIBBERT, F.A., ORME B.J., PETTIT, M., RUSHTON, D. and SWITSUR, V.R., 1973. Prehistoric Roads and Tracks in Somerset, England: 3. The Sweet Track. Proceedings of the Prehistoric Society,39, pp. 256-293.
ELBURG, R., HEIN, W., PROBST, A. and WALTER, P., 2015. Field Trials in Neolithic Woodworking: (Re)Learning to use Early Neolithic stone adzes. In: R. Kelm, ed. 2015. Archaeology and Crafts: Experiences and Experiments on traditional Skills and Handicrafts in Archaeological Open-Air Museums in Europe. Husum: Husum Druck- und Verlagsgesellschaft. pp.62-77
ENNOS, A.R., 2012. Solid Biomechanics.Princeton: Princeton University Press.
ENNOS, A.R. and Van CASTEREN, A., 2010. Transverse stresses and modes of failure in tree branches and other beams. Proceedings of the Royal Society of London B: Biological Sciences, 277, pp. 1253-1258.
EVANS, J., 1897. The ancient stone implements, weapons and ornaments of Great Britain. 2nd ed. London: Longmans, Green, and Co.
GORDON, J.E., 1978. Structures: Or Why Things Don't Fall Down . London: Penguin Books.
GURNEY, C. and HUNT, J., 1967. Quasi-static crack propagation. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences , 299, pp. 508-524.
HARDING, P., 2014. Working with flint tools: personal experience making a Neolithic axe haft. Lithics: The Journal of the Lithics Study Society, 35, pp. 40-53.
HOADLEY, R.B., 2000. Understanding Wood: A Craftsman’s Guide to Wood Technology. Newtown, C.T.: Taunton Press.
JØRGENSEN, S., LERCHE, G., TROELS-SMITH, J.A. and STEENSBERG, A., 1985. Tree-felling: With Original Neolithic Flint-axes in Draved Wood: Report on the Experiments in 1952-54. Copenhagen: National Museum of Denmark.
MATHIEU, J.R. and MEYER, D.A., 1997. Comparing Axe Heads of Stone, Bronze, and Steel: Studies in Experimental Archaeology. Journal of Field Archaeology, 24, pp. 333-351.
MATTHECK, C., 1998. Design in nature: learning from trees. Berlin: Springer.
MATTHECK, C. and KUBLER, H., 1995. Wood: The Internal Optimization of Trees . Berlin: Springer.
MYTTING, L., 2015. Norwegian Wood : Chopping, Stacking, and Drying Wood the Scandinavian Way .London: MacLehose Press.
OBREIMOFF, J.W., 1930. The splitting strength of mica. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character , 127, pp. 290- 298.
ÖZDEN, S. and ENNOS, A.R., 2014. Understanding the Function of Rays and Wood Density on Transverse Fracture Behaviour of Green Wood in Three Species. Journal of Agricultural Science and Technology B, 4, pp. 731-743.
ÖZDEN, S., ENNOS, A.R. and CATTANEO, M.E.G.V., 2017. Transverse fracture properties of green wood and anatomy of six temperate tree species. Forestry: An International Journal of Forest Research, 90, pp. 58-69.
ÖZDEN, S., SLATER, D. and ENNOS, A.R., 2017. Fracture properties of green wood formed within the forks of hazel (Corylus avellana L.). Trees, 31, pp. 903-917.
REITERER, A., BURGERT, I., SINN, G. and TSCHEGG, S., 2002. The radial reinforcement of the wood structure and its implication on mechanical and fracture mechanical properties – A comparison between two tree species. Journal of Materials Science, 37, pp. 935-940.
SHERIDAN, A., 1992. Scottish stone axeheads: some new work and recent discoveries. In: N. M. Sharples and A. Sheridan, eds. 1992. Vessels for the Ancestors: Essays on the Neolithic of Britain and Ireland in Honour of Audrey Henshall. Edinburgh: Edinburgh University Press. pp. 194-212.
SLATER, D., BRADLEY, R.S., WITHERS, P.J. and ENNOS, A.R., 2014. The anatomy and grain pattern in forks of hazel (Corylus avellana L.) and other tree species. Trees,28, pp. 1437-1448.
SLATER, D. and ENNOS, A.R., 2015. Interlocking wood grain patterns provide improved wood strength properties in forks of hazel (Corylus avellana L.). Arboricultural Journal: The International Journal of Urban Forestry , 37, pp. 21-32.
TAYLOR, M., 1998. Wood and Bark from the Enclosure Ditch. In: F. Pryor, ed. 1998. Etton: Excavations at a Neolithic causewayed enclosure near Maxey Cambridgeshire, 1982-7 . Swindon: English Heritage Publishing. pp. 115-160
TAYLOR, M., 2011. Waterlogged wood. In: G. Momber, D. Tomalin, R. Scaife, J. Satchell and J. Gillespie, eds. 2011. Mesolithic Occupation at Bouldnor Cliff and the Submerged Prehistoric Landscapes of the Solent . York: Council for British Archaeology. pp.84-89.
TEGEL, W., ELBURG, R., HAKELBERG, D., STÄUBLE, H. and BÜNTGEN, U., 2012. Early Neolithic Water Wells Reveal the World’s Oldest Wood Architecture. PLoS ONE, 7, e51374.
Van CASTEREN, A., SELLERS, W.I., THORPE, S.K.S., COWARD, S., CROMPTON, R.H. and ENNOS, A.R., 2012. Why don’t branches snap? The mechanics of bending failure in three temperate angiosperm trees.Trees, 26,pp. 789-797.
WILLIAMS, J.G. and PATEL, Y., 2016. Fundamentals of cutting. Interface Focus, 6, 20150108.
YERKES, R.W., BARKAI, R., GOPHER, A. and YOSEF, O.B., 2003. Microwear analysis of early Neolithic (PPNA) axes and bifacial tools from Netiv Hagdud in the Jordan Valley, Israel. Journal of Archaeological Science,30, pp. 1051-1066.

